Summarize Argument
The economist tells us that the current recession appears to be ending. To support this, we get a chain of reasoning. First, a fact: consumers have started purchasing more durable goods. Second, an interpretation based on this fact (i.e. a sub-conclusion): consumers expect economic growth soon. And with this, the economist supports the conclusion that the recession seems to be ending.
Identify Argument Part
The claim that consumers are buying more durable goods than before is a factual premise. More specifically, it is a premise that supports a sub-conclusion (consumers expect economic growth), which then supports the main conclusion (the recession is ending).
A
It is the phenomenon that the argument seeks to explain.
The argument isn’t really trying to explain a phenomenon. Instead, the economist is trying to make a prediction about the future based on current data. This answer choice just isn’t accurate to the argument.
B
Its truth is required in order for the argument’s conclusion to be true.
The conclusion that the recession seems to be ending may be supported by the claim about consumers’ purchases, but that doesn’t mean one is required for the other. The economist could be mistaken about the consumers but the conclusion could still be true.
C
It is an inference drawn from the premise that the recession seems to be ending.
Like (D), this gets things backwards: the claim that the recession seems to be ending is the main conclusion, not a premise. Also, the claim about consumers’ purchases is stated as a fact, not inferred from something else.
D
It is an inference drawn from the premise that consumers expect economic growth in the near future.
Like (C), this gets things backwards: the claim about consumers’ expectations is a sub-conclusion supported by the claim about consumers’ purchases. Also, the claim about consumers’ purchases is a factual premise, not an inference.
E
It is the primary evidence from which the argument’s conclusion is drawn.
This accurately describes the role of the claim about consumers’ purchases. It’s the only pure factual premise in the argument, meaning it’s our only piece of hard evidence. The rest of the argument is just a series of inferences drawn from this evidence.
Summary
Special cotton from green/brown fibers havae been around since 1930s. Only recently, this special cotton became commercially feasible when a long-fibered kind that can be spun by machine came about. This long-fibered kind doesn’t need to be dyed, which is why processing plants don’t need to spend money on dyeing. In addition, since the long-fibered variety doesn’t need to use dyes, plants don’t need to get rid of leftover dye from processing, which avoids some ecological damage.
Very Strongly Supported Conclusions
There’s no obvious conclusion to draw from these facts. I’d go into the answers thinking, “There are at least some advantages to the long-fibered variety of cotton from green/brown fibers over the non-long-fibered variety of that cotton.” But the correct answer could be unexpected.
A
It is ecologically safer to process long-fibered cotton than short-fibered cotton.
We know that the long-fibered green/brown cotton doesn’t have a certain ecological risk (because it doesn’t require dyes). But this doesn’t extend to long-fibered cotton that isn’t green/brown. We don’t know about ecological risks of other kinds of long cotton.
B
Green and brown cottons that can be spun only by hand are not commercially viable.
Strongly supported, because the green/brown cotton “only recently” became commercially feasible, and this happened after a variety that could be machine-spun “finally” came about. This suggests that before a machine-spun version came about, it wasn’t commercially viable.
C
Hand-spun cotton is more ecologically safe than machine-spun cotton.
We don’t get a comparison concerning ecological damage between machine-spun vs. hand-spun cotton. All we know about ecological risk is that if you don’t have to use dyes, you avoid at least one ecological risk.
D
Short-fibered regular cottons are economically competitive with synthetic fabrics.
We don’t get any comparison between short-fibered cottons and synthetic fabrics.
E
Garments made of green and brown cottons are less expensive than garments made of regular cotton.
We know that processing plants don’t need to spend on dyes for creating green/brown cotton. This doesn’t suggest that clothes from green/brown cotton are less expensive, however. There are many other costs that go into clothing; we can’t go from the lack of one specific cost with respect to the cotton to a claim about overall cost of clothing from the green/brown cotton compared to other clothing.
Summary
The author concludes that mathematical propositions cannot be known to be true. This is based on the fact that mathematical propositions cannot be proven true by observation.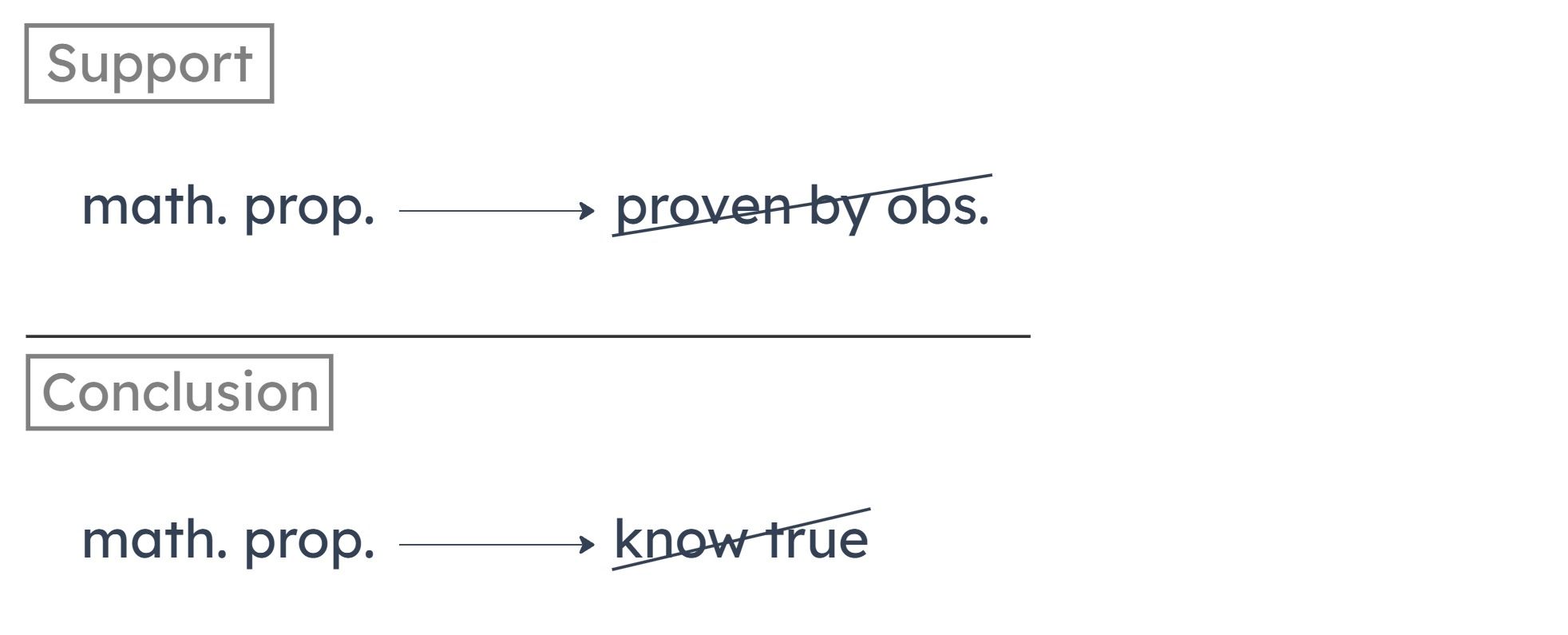

Missing Connection
There’s a difference between being impossible to prove true by observation and being impossible to know is true. What if mathematical propositions are impossible to prove true by observation, but are possible to know through some other method besides observation, such as through logic? This is the flaw in the argument.
To make the argument valid, we want to know that if something is impossible to prove true by observation, then it is impossible to know is true. In other words, we want to know that in order to know that something is true, we must be able to prove it true through observation.
To make the argument valid, we want to know that if something is impossible to prove true by observation, then it is impossible to know is true. In other words, we want to know that in order to know that something is true, we must be able to prove it true through observation.
A
Only propositions that can be proven true can be known to be true.
(A) doesn’t make the argument valid, because we don’t know that mathematical propositions can never be proven true. We do know that they can’t be proven true through observation; but they might be provable through some other method besides observation.
B
Observation alone cannot be used to prove the truth of any proposition.
(B) leaves open the possibility that we might be able to know the truth of math propositions through other methods besides observation.
C
If a proposition can be proven true by observation, then it can be known to be true.
This is the reverse of what we’re looking for. We want to know that in order for something to be known true, it must be provable by observation. But (C) tells us that provability by observation is sufficient to know something is true. That doesn’t establish that if something is impossible to prove through observation, we can’t know it’s true.
D
Knowing a proposition to be true is impossible only if it cannot be proven true by observation.
The is the reverse of what we’re looking for. (D) tells us that if we can’t know something to be true, then it can’t be proven true by observation. But (D) leaves open the possibility that some things that can’t be proven true by observation might still be knowable as true through some other method.
E
Knowing a proposition to be true requires proving it true by observation.
(E) tells us that provability through observation is necessary in order to know a proposition to be true. This establishes that if we can’t prove something true through observation — as is the case with math propositions — then we can’t know it to be true.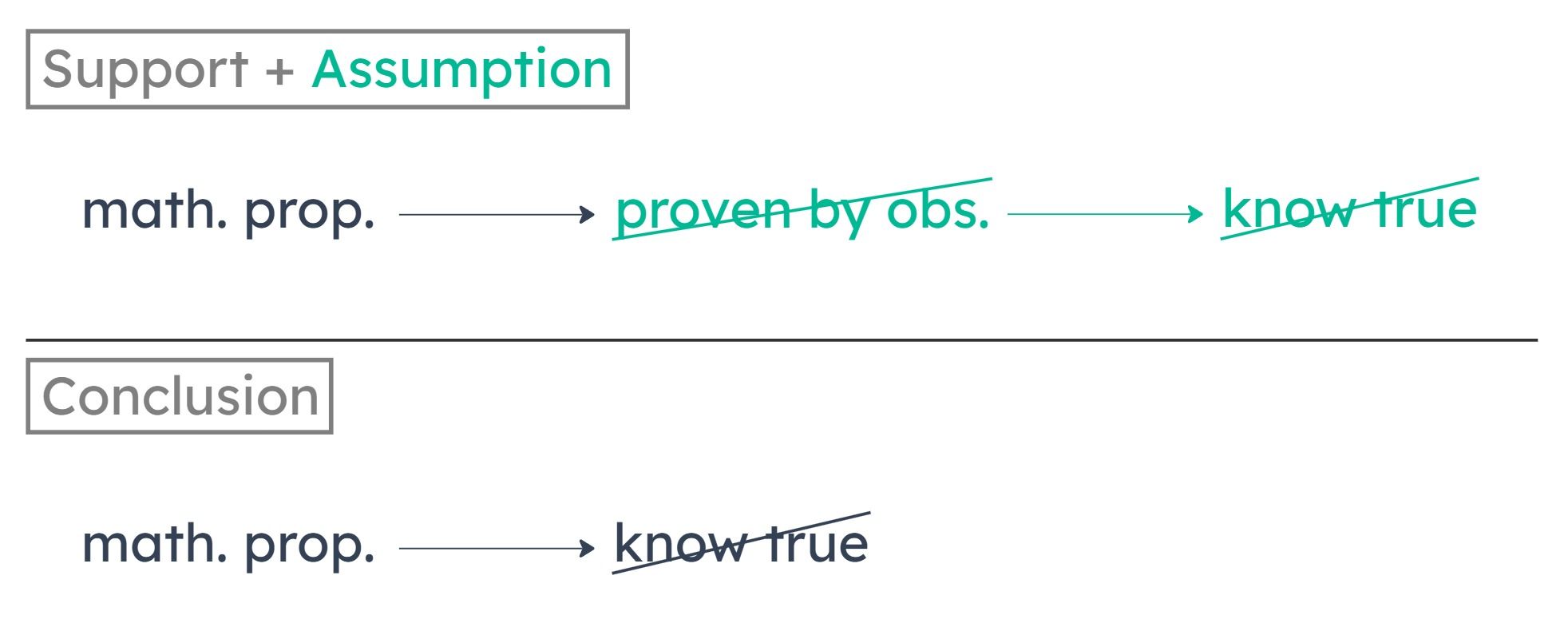

Note: At 0:34, J.Y. said that "no" was "negate sufficient" when he meant to say "negate necessary".
Summary
The stimulus can be diagrammed as follows:
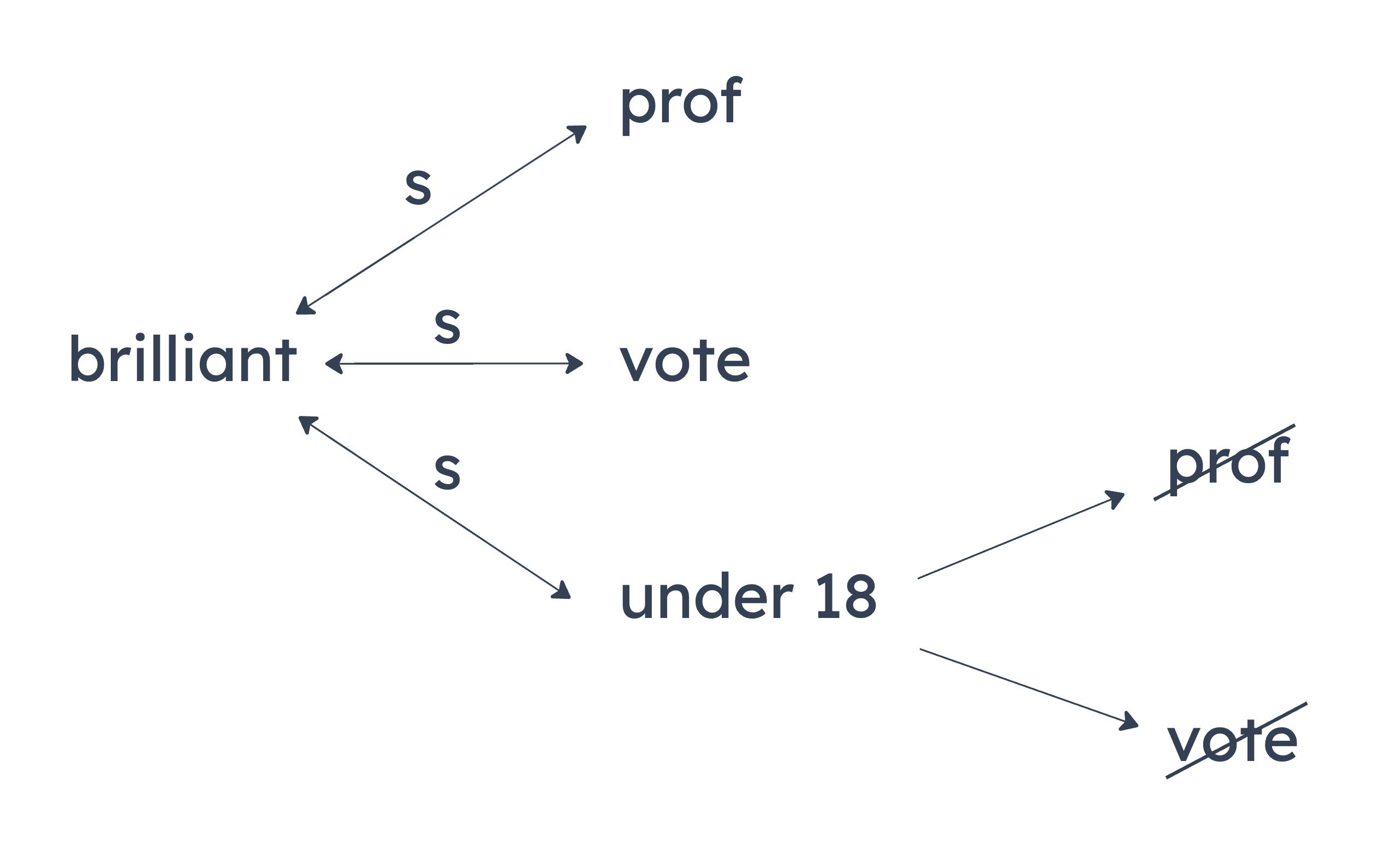

Notable Valid Inferences
Some brilliant people are not professors.
Some brilliant people cannot legally vote.
Some brilliant people cannot legally vote.
A
No professors are eighteen-year-olds.
Could be false. Some professors could be eighteen-year-olds. We know that no professors are under eighteen, but this leaves room for the possibility that some professors are exactly eighteen.
B
All brilliant people are either professors, legal voters, or under eighteen.
Could be false. We know that some brilliant people are professors, legal voters, and/or under eighteen. But this may not be an exhaustive list. There could be brilliant people out there who are none of these three things.
C
Some legal voters are not professors.
Could be false. It’s possible that all legal voters are professors. The only things we can say for sure about legal voters are that some of them are brilliant people, and none of them are under eighteen.
D
Some professors are neither legal voters nor brilliant people.
Could be false. It’s possible that all professors are either legal voters or brilliant people, or both. The only things we can say for sure about professors are that at least some of them are brilliant people, and none of them are under eighteen.
E
Some brilliant people are neither professors nor legal voters.
Must be true. Some brilliant people are under eighteen, meaning they are not professors and cannot legally vote.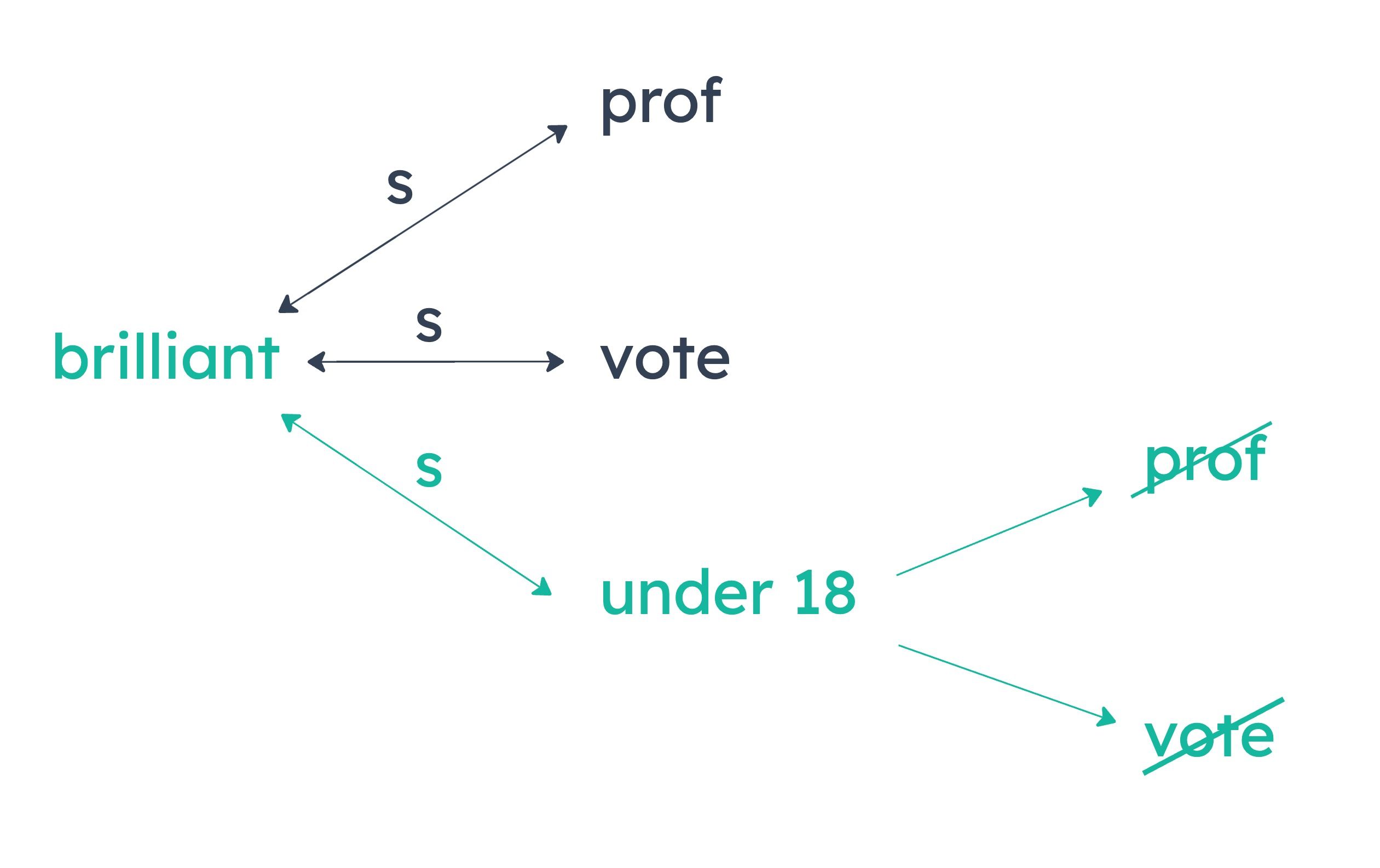

Summary
The conclusion is that there shouldn’t be a legal prohibition against gambling. This is based on the following:
Gambling laws can’t be enforced.
If a law is not effective, it should not be a law.

Gambling laws can’t be enforced.
If a law is not effective, it should not be a law.

Missing Connection
The second premise (if a law is not effective, it should not be a law) gives us a way to prove that something should be a law. So if we can learn that gambling laws aren’t effective, we can prove that they shouldn’t be laws. The first premise establishes that gambling laws can’t be enforced. There’s a missing link between “can’t be enforced” and “not effective.” We should go to the answer looking for “If a law can’t be enforced, then it’s not effective.” Or, the contrapositive: “If a law is effective, it has to be enforceable.”
A
No effective law is unenforceable.
This establishes that if a law is effective, it must NOT be UNenforceable. Take away the double negative and this means, if a law is effective it must be enforceable. This establishes that since gambling laws aren’t enforceable, they cannot be effective. 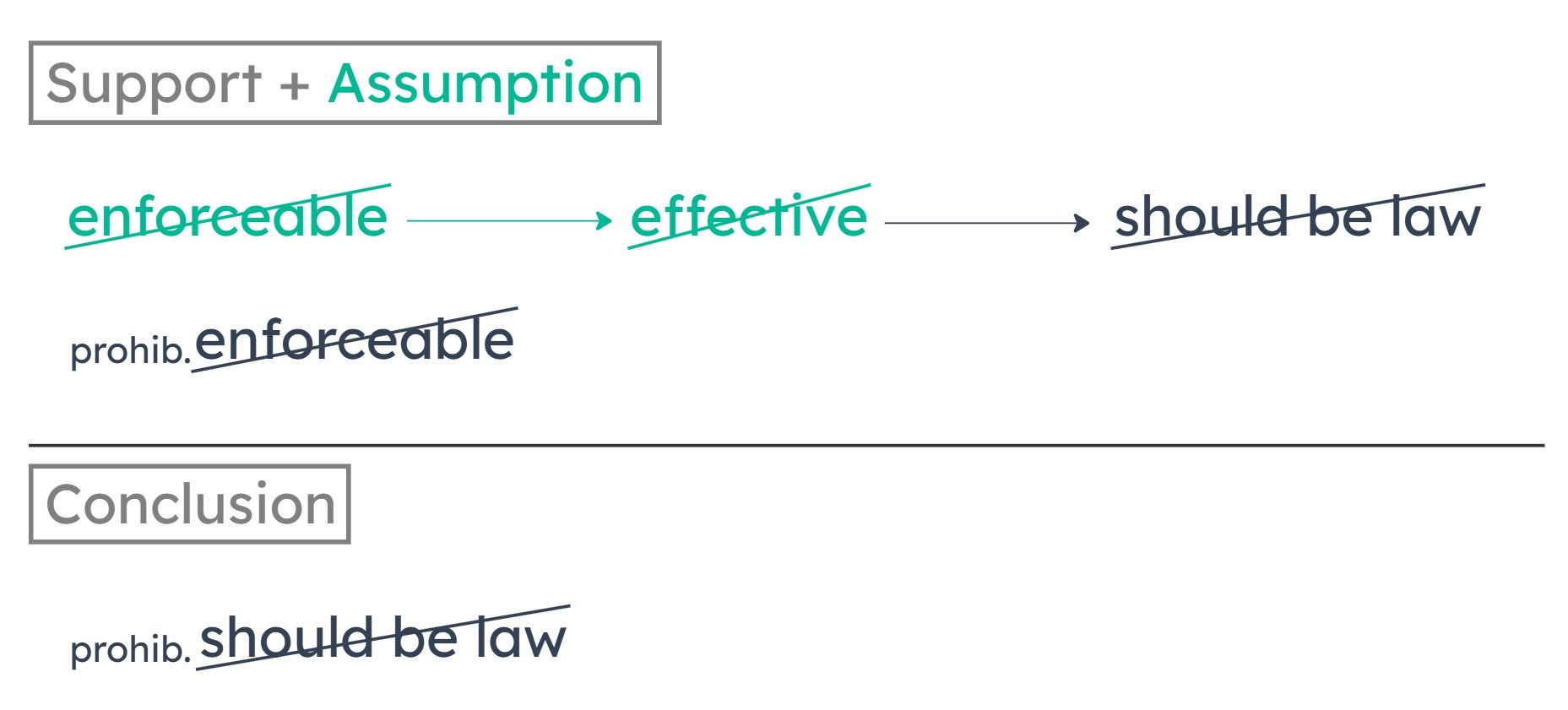

B
All enforceable laws are effective.
This means that if a law is enforceable, it’s effective. This reverses what we’re looking for. (B) doesn’t prove that if a law isn’t enforceable, it can’t be effective. In other words, (B) still allows for gambling laws to be effective, even though they’re not enforceable.
C
No legal prohibitions against gambling are enforceable.
A premise already establishes that gambling prohibitions are not enforceable. (C) doesn’t establish that the gambling prohibitions are not EFFECTIVE. There’s a difference between “not enforceable” and “not effective.”
D
Most citizens must agree with a law for the law to be effective.
The premises don’t give us enough to establish that most citizens don’t agree with gambling laws; so (D) doesn’t establish that gambling laws aren’t effective. We know that most citizens recognize that they’re not enforceable, but this doesn’t imply that they don’t agree with the laws.
E
Most citizens must agree with a law for the law to be enforceable.
The premises already establish that gambling laws are not enforceable. (E) doesn’t establish that the laws are not EFFECTIVE. There’s a difference between “not enforceable” and “not effective.”
Summary
The author concludes that some students with part-time jobs do not walk to school. His reasoning is that every student who walks to school goes home for lunch. Or, in contrapositive form, that all students who don’t go home for lunch don’t walk to school.
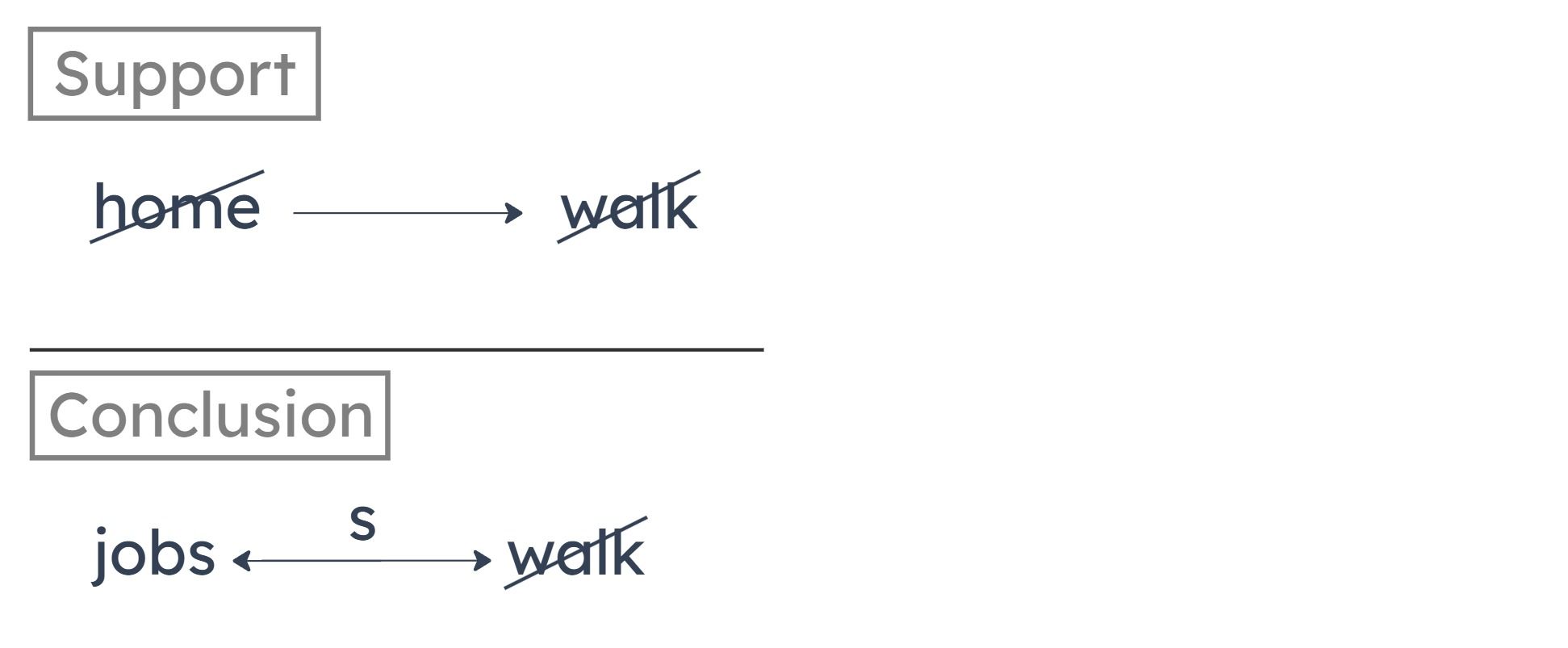

Missing Connection
The conclusion is about students with part-time jobs, but they aren’t mentioned in the premise. We need to bridge this gap to reach the conclusion that some students with part-time jobs do not walk to school.
By taking the contrapositive of the premise, we inferred that all students who don’t go home for lunch don’t walk to school. So, if at least some students with part-time jobs don’t go home for lunch, then some of them wouldn’t walk to school. This would guarantee the argument’s conclusion.
By taking the contrapositive of the premise, we inferred that all students who don’t go home for lunch don’t walk to school. So, if at least some students with part-time jobs don’t go home for lunch, then some of them wouldn’t walk to school. This would guarantee the argument’s conclusion.
A
Some students who do not have part-time jobs go home for lunch.
This can’t be correct, because it tells us about some students who don’t have part-time jobs. Our conclusion is about students who do have part-time jobs. A “some” statement’s contrapositive isn’t automatically valid. So this tells us nothing about students with part-time jobs.
B
Every student who goes home for lunch has a part-time job.
This doesn’t help us reach our conclusion, because all it lets us infer is that some students with part-time jobs go home for lunch. We want to conclude that some students with part-time jobs do not walk to school.
C
Some students who do not have part-time jobs do not go home for lunch.
This can’t be correct, because it tells us about some students who don’t have part-time jobs. Our conclusion is about students who do have part-time jobs. A “some” statement’s contrapositive isn’t automatically valid. So this tells us nothing about students with part-time jobs.
D
Some students who do not go home for lunch have part-time jobs.
Every student who doesn’t go home for lunch doesn’t walk to school. So, if some students with part-time jobs don’t go home for lunch, some students with part-time jobs don’t walk to school. Note that “some” is bidirectional: saying some As are Bs is equivalent to saying that some Bs are As.
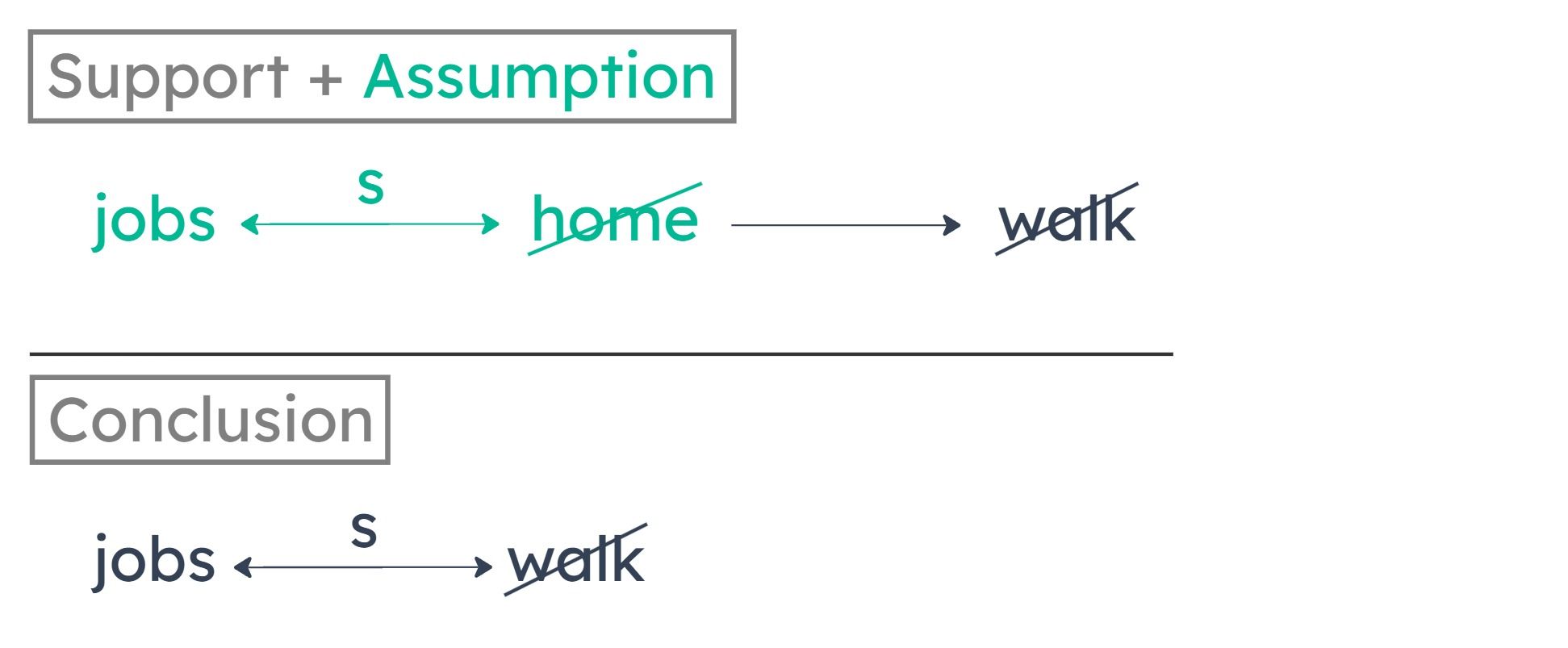

E
Every student who goes home for lunch walks to school.
This doesn’t mention students with part-time jobs, so it can’t be correct. We need an answer that bridges the gap between the premise and the conclusion.