LSAT 101 – Section 2 – Question 24

LSAT 101 - Section 2 - Question 24

December 1997

You need a full course to see this video. Enroll now and get started in less than a minute.

Ask a tutor

Target time: 0:57

This is question data from the 7Sage LSAT Scorer. You can score your LSATs, track your results, and analyze your performance with pretty charts and vital statistics - all with a Free Account ← sign up in less than 10 seconds

Question
QuickView		 Type Tags Answer
Choices		 Curve Question
Difficulty		 Psg/Game/S
Difficulty		 Explanation
PT101 S2 Q24
+LR
Sufficient assumption +SA
Conditional Reasoning +CondR
Link Assumption +LinkA
A
10%
166
B
8%
161
C
6%
160
D
8%
163
E
68%
170
154
162
170
 +Hardest 150.088 +SubsectionMedium

No mathematical proposition can be proven true by observation. It follows that it is impossible to know any mathematical proposition to be true.

Summary
The author concludes that mathematical propositions cannot be known to be true. This is based on the fact that mathematical propositions cannot be proven true by observation.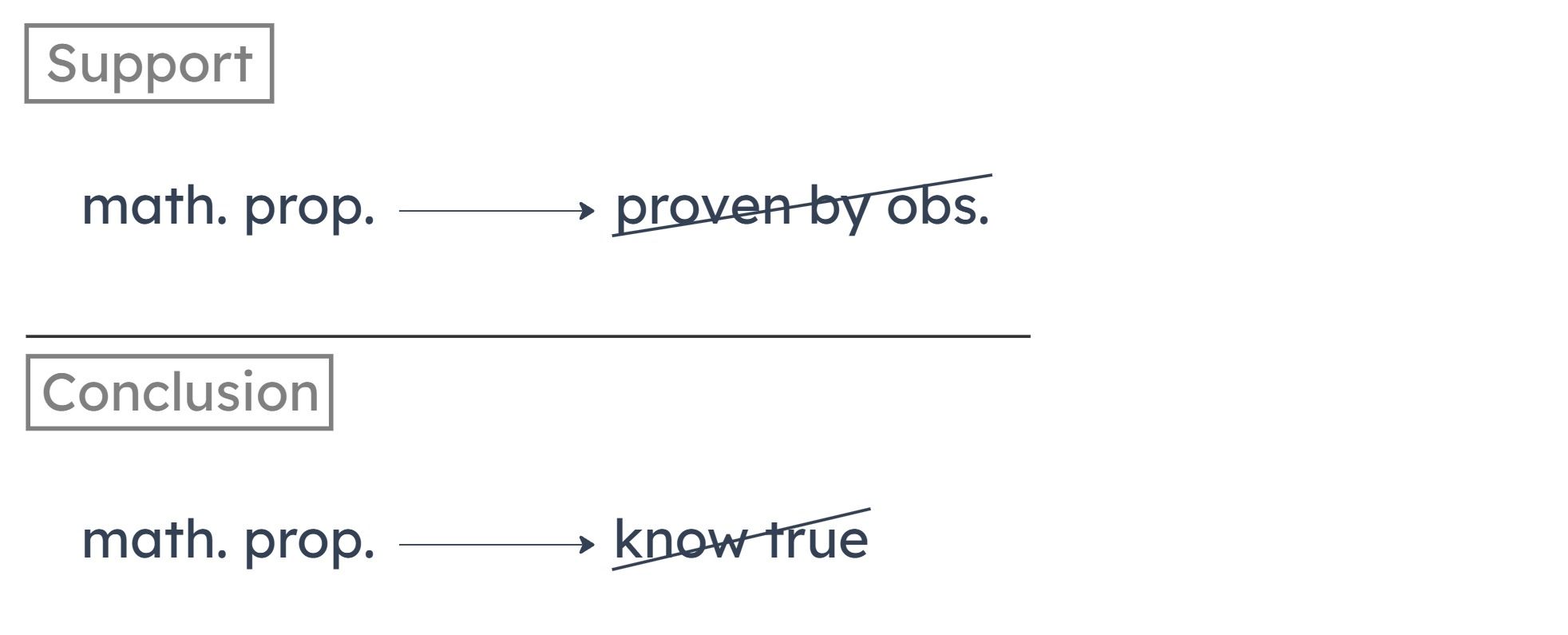

Missing Connection
There’s a difference between being impossible to prove true by observation and being impossible to know is true. What if mathematical propositions are impossible to prove true by observation, but are possible to know through some other method besides observation, such as through logic? This is the flaw in the argument.
To make the argument valid, we want to know that if something is impossible to prove true by observation, then it is impossible to know is true. In other words, we want to know that in order to know that something is true, we must be able to prove it true through observation.

A
Only propositions that can be proven true can be known to be true.
(A) doesn’t make the argument valid, because we don’t know that mathematical propositions can never be proven true. We do know that they can’t be proven true through observation; but they might be provable through some other method besides observation.
B
Observation alone cannot be used to prove the truth of any proposition.
(B) leaves open the possibility that we might be able to know the truth of math propositions through other methods besides observation.
C
If a proposition can be proven true by observation, then it can be known to be true.
This is the reverse of what we’re looking for. We want to know that in order for something to be known true, it must be provable by observation. But (C) tells us that provability by observation is sufficient to know something is true. That doesn’t establish that if something is impossible to prove through observation, we can’t know it’s true.
D
Knowing a proposition to be true is impossible only if it cannot be proven true by observation.
The is the reverse of what we’re looking for. (D) tells us that if we can’t know something to be true, then it can’t be proven true by observation. But (D) leaves open the possibility that some things that can’t be proven true by observation might still be knowable as true through some other method.
E
Knowing a proposition to be true requires proving it true by observation.
(E) tells us that provability through observation is necessary in order to know a proposition to be true. This establishes that if we can’t prove something true through observation — as is the case with math propositions — then we can’t know it to be true.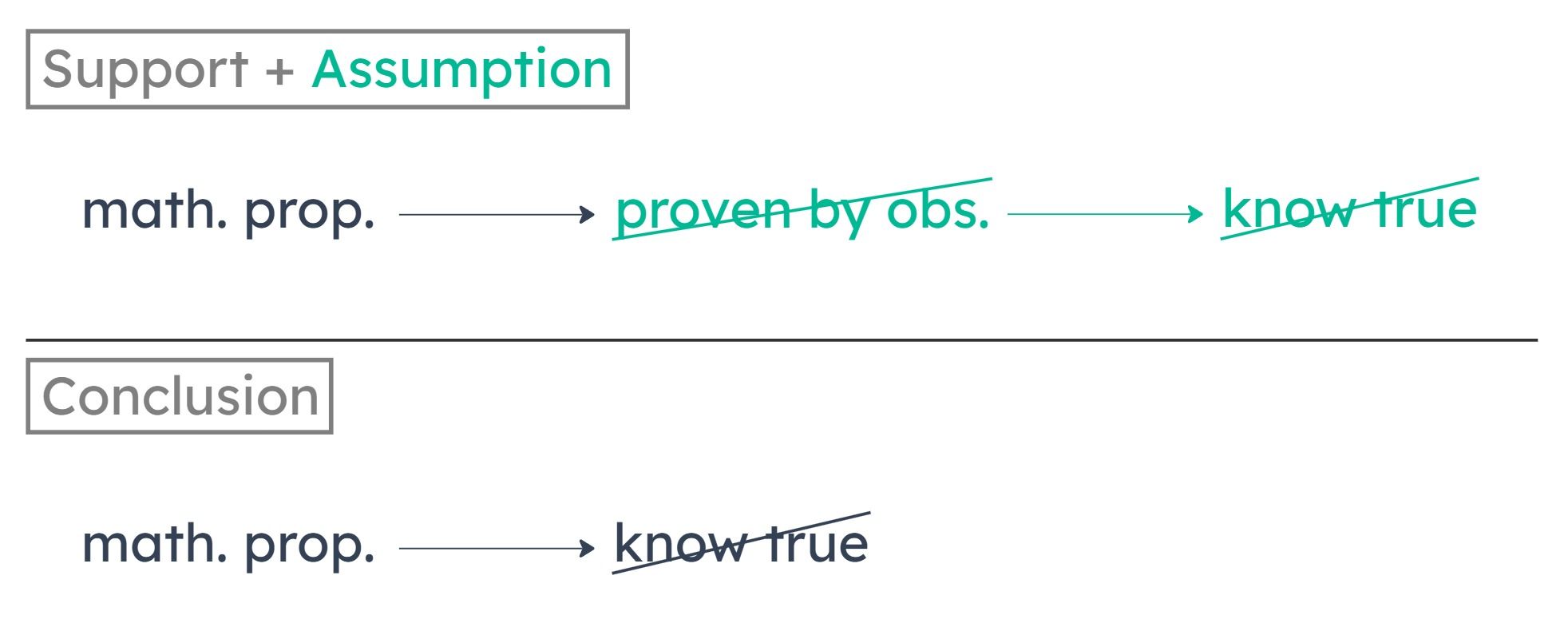

Note: At 0:34, J.Y. said that "no" was "negate sufficient" when he meant to say "negate necessary".

Take PrepTest

Review Results

LSAT PrepTest 101 Explanations

Section 1 - Reading Comprehension

Section 2 - Logical Reasoning

Section 3 - Logical Reasoning

Section 4 - Reading Comprehension

Get full LSAT course

Leave a Reply