Note: At 0:34, J.Y. said that "no" was "negate sufficient" when he meant to say "negate necessary".
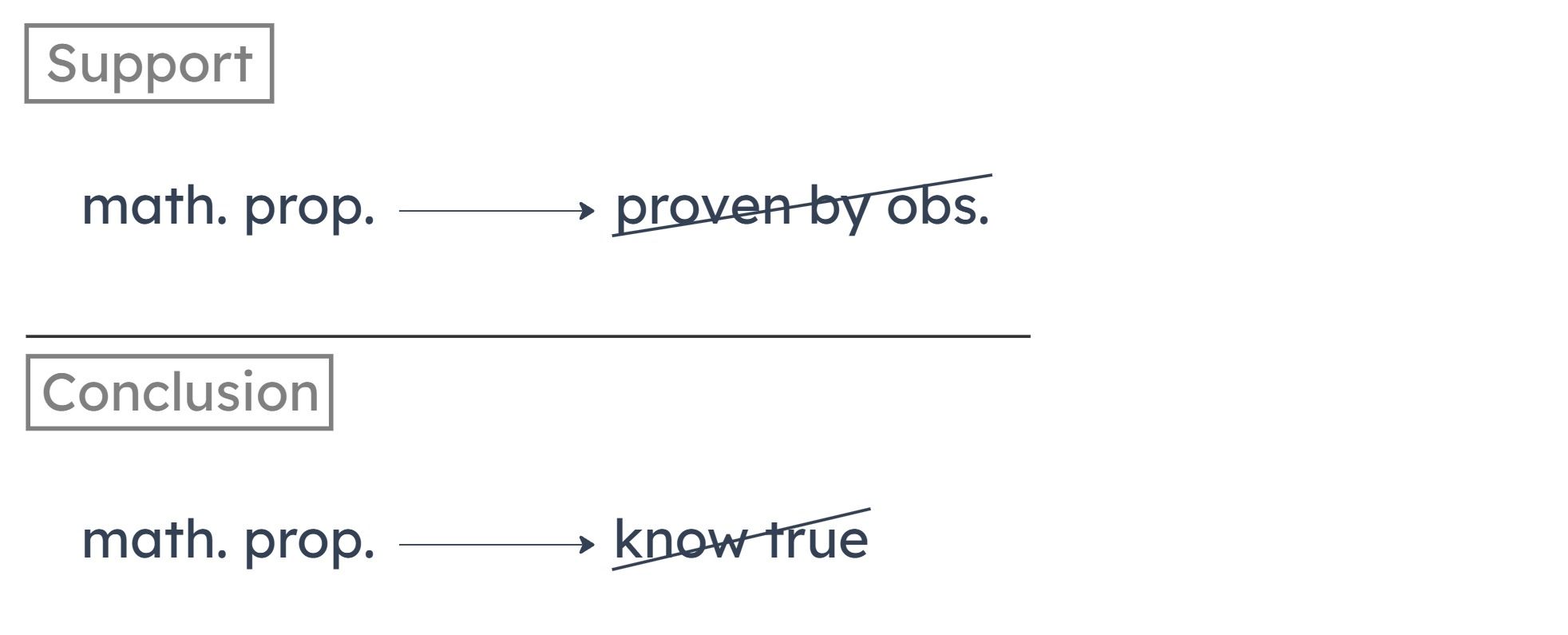
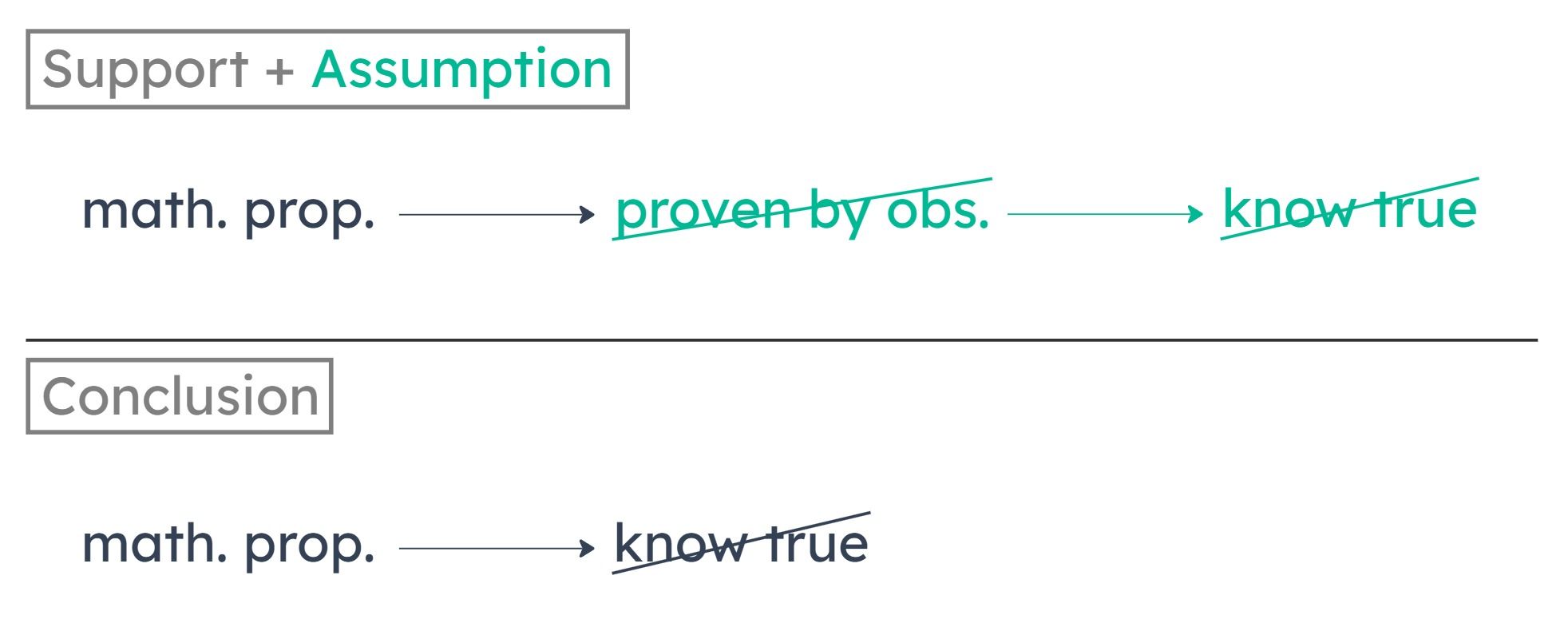
To make the argument valid, we want to know that if something is impossible to prove true by observation, then it is impossible to know is true. In other words, we want to know that in order to know that something is true, we must be able to prove it true through observation.
A
Only propositions that can be proven true can be known to be true.
B
Observation alone cannot be used to prove the truth of any proposition.
C
If a proposition can be proven true by observation, then it can be known to be true.
D
Knowing a proposition to be true is impossible only if it cannot be proven true by observation.
E
Knowing a proposition to be true requires proving it true by observation.
Note: At 0:34, J.Y. said that "no" was "negate sufficient" when he meant to say "negate necessary".
Numismatist: In medieval Spain, most gold coins were minted from gold mined in West Africa, in the area that is now Senegal. The gold mined in this region was the purest known. Its gold content of 92 percent allowed coins to be minted without refining the gold, and indeed coins minted from this source of gold can be recognized because they have that gold content. The mints could refine gold and produced other kinds of coins that had much purer gold content, but the Senegalese gold was never refined.
Summary
A numismatist tells us that most medieval Spanish gold coins were made of gold mined in Senegal. The Senegalese gold was 92 percent pure, which is so pure that it was never refined further before minting the coins. Gold from other sources, however, could be refined and thus still be minted into coins with a gold content higher than the Senegalese gold.
Strongly Supported Conclusions
The strongly supported conclusions that we can find in these facts are:
Most gold coins minted in medieval Spain had a gold content of 92 percent and were made of unrefined gold.
Medieval Spanish mints were able to refine gold from a purity less than 92 percent to a purity above 92 percent.
Some coins were minted in medieval Spain with a gold content higher than 92 percent, and were made of gold that was originally less than 92 percent pure.
A
Coins minted from Senegalese gold all contained the same weight, as well as the same proportion, of gold.
This is not supported. The stimulus never indicates the weight of different coins, only the purity of the gold used to make them. We have no idea whether all coins made from Senegalese gold had the same total weight.
B
The source of some refined gold from which coins were minted was unrefined gold with a gold content of less than 92 percent.
This is strongly supported. We know that 92 percent pure Senegalese gold, the purest known, was never refined, so any refined gold coins had to come from a less-than-92-percent pure source. And the facts state that some more-than-92-percent pure (i.e. refined) coins were made.
C
Two coins could have the same monetary value even though they differed from each other in the percentage of gold they contained.
This is not supported. The facts given don’t suggest anything about the monetary value of different coins, so we just can’t say how that relates to gold percentage.
D
No gold coins were minted that had a gold content of less than 92 percent.
This is not supported. We know that some coins were minted with a gold content of 92 percent and that some were minted with an even higher gold content, but the author never indicates whether or not coins were minted with a lower gold content.
E
The only unrefined gold from which coins could be minted was Senegalese gold.
This is not supported. Just because medieval Spanish mints made coins out of unrefined Senegalese gold, that doesn’t mean they never used other unrefined gold. Maybe they had a source of 90 percent pure gold that they also didn’t refine. We just don’t know!